[فوزى عبده]

Choupei Proof


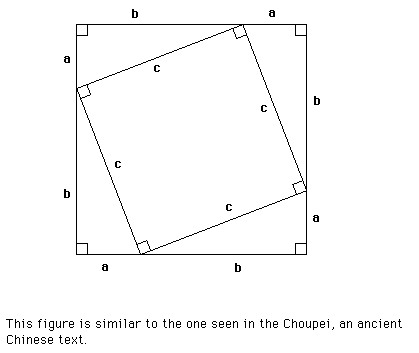
Looking at the diagram, the figure is made up of a large square, small square, and four right triangles. The steps for solving the proof:

• The area of the large square = (a + b)(a + b) = a^2 + 2ab + b^2.
• The area of the small square = (c)(c) = c^2.
• The area of the four triangles = 4(.5ab) = 2ab.
• The area of large square - area of 4 triangles = area of the small square (a^2 + 2ab + b^2) - (2ab) = c^2
  a^2 + b^2 = c^2
• Therefore, the sum of the squares of the sides of a right triangle equals the square of the hypotenuse.