
Let ABC represent a right triangle, with the right angle located at C, as shown on the figure. We draw the altitude from point C, and call H its intersection with the side AB. Point H divides the length of the hypotenuse c into parts d and e. The new triangle ACH is similar to triangle ABC, because they both have a right angle (by definition of the altitude), and they share the angle at A, meaning that the third angle will be the same in both triangles as well, marked as θ in the figure. By a similar reasoning, the triangle CBH is also similar to ABC. The proof of similarity of the triangles requires the Triangle postulate: the sum of the angles in a triangle is two right angles, and is equal to the parallel postulate. Similarity of the triangles leads to the equality of ratios of corresponding sides
:
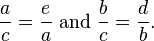
The first result equates the cosine of each angle θ and the second result equates the sines.
These ratios can be written as:

Summing these two equalities, we obtain
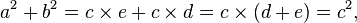
which, tidying up, is the Pythagorean theorem
:
