[hohaho]

المشاركة الأصلية كتبت بواسطة MathPrince

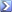
Permutation:

How many 3-letter code symbols can be formed with the letters A, B, C </div></div>

<div align="left">

without repetition. We can select any of the 3 letters for the first letter in the symbol. Once this letter has been selected, the second must be selected from the 2 remaining letters. After this, the third letter is already determined, since only 1 possibility is left. That is, we can place any of the 3 letters in the first box, either of the remaining 2 letters in the second box, and the only remaining letter in the third box. The possibilities can be arrived at using a tree diagram, as shown below.

We see that there are 6 possibilities. The set of all the possibilities is
{ABC, ACB, BAC, BCA, CAB,CBA}

Combination:
EXAMPLE 1 Find all the combinations of 3 letters taken from the set of 5 letters
{A, B,C, D, E}
Solution The combinations are
{A,B,C} {A,B,D}
{A,B, E} {A,C,D}
{A,C, E} {A,D, E}
{B,C,D} {B,C, E}
{B,D, E} {C,D, E}
There are 10 combinations of the 5 letters taken 3 at a time

When we find all the combinations from a set of 5 objects taken 3 at a time, we are finding all the 3-element subsets. When a set is named, the order of the elements is

<div align=&quot;left&quot;>not considered. Thus, {A,C,B}names the same set as {A,B,C}.

thank you very much for the great effort you exerted with me