|
||||||
| أرشيف المنتدى هنا نقل الموضوعات المكررة والروابط التى لا تعمل |
|
|
أدوات الموضوع | ابحث في الموضوع | انواع عرض الموضوع |
|
#4
|
|||
|
|||
|
Permutation: How many 3-letter code symbols can be formed with the letters A, B, C without repetition. We can select any of the 3 letters for the first letter in the symbol. Once this letter has been selected, the second must be selected from the 2 remaining letters. After this, the third letter is already determined, since only 1 possibility is left. That is, we can place any of the 3 letters in the first box, either of the remaining 2 letters in the second box, and the only remaining letter in the third box. The possibilities can be arrived at using a tree diagram, as shown below. 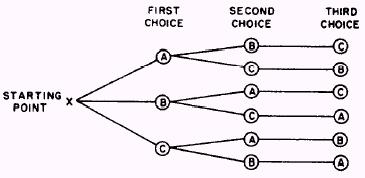 We see that there are 6 possibilities. The set of all the possibilities is {ABC, ACB, BAC, BCA, CAB,CBA} Combination: EXAMPLE 1 Find all the combinations of 3 letters taken from the set of 5 letters {A, B,C, D, E} Solution The combinations are {A,B,C} {A,B,D} {A,B, E} {A,C,D} {A,C, E} {A,D, E} {B,C,D} {B,C, E} {B,D, E} {C,D, E} There are 10 combinations of the 5 letters taken 3 at a time When we find all the combinations from a set of 5 objects taken 3 at a time, we are finding all the 3-element subsets. When a set is named, the order of the elements is not considered. Thus, {A,C,B}names the same set as {A,B,C}. |
| العلامات المرجعية |
«
الموضوع السابق
|
الموضوع التالي
»
|
|
جميع الأوقات بتوقيت GMT +2. الساعة الآن 02:28 PM.









 العرض الشجري
العرض الشجري